
But the way the discrete Fourier transform work is that it computes the frequencies multiple of 1/n (for n data points). Since I'm interested in finding the period of the signal (the byte length of a row of pixels), I want to plot the spectrogram with period length on the y axis, not the frequency.
Since finding the length of a mostly repeating pattern looks like finding a frequency, I tried to use a Fourier transform with 1 byte = 1 sample and plot the absolute value of the spectrum.īut the main problem is the period resolution. I tried using FFT and autocorrelation, but they do not show the kind of accuracy I'm after.
That means processing a few tens of MB per second. As an order of magnitude, I would like to be able to find images of width 2048 in RGBA (8192 bytes per row) in a 4GB file in a few minutes. The problem I have right now is to find a method to compute that "kind of spectrogram" accurately and quickly. Then I'd just have to look for horizontal lines in it. More precise a heatmap where the shade show how likely it is for the block of data # x to be part of an image of width y bytes, with x and y the axis of the spectrogram. If I find a large enough number of lines of the same size, then I let the user fiddle around with an interactive tool and see if it decodes to something interesting.įor this, I would compute a kind of spectrogram. My idea was to rely on the fact that a row of pixels is similar to the next one. If I can do this, I hope to find the content of the windows, at least partially. So I'd like to reformulate the problem as finding raw images (think matrix of pixels) in a large file.
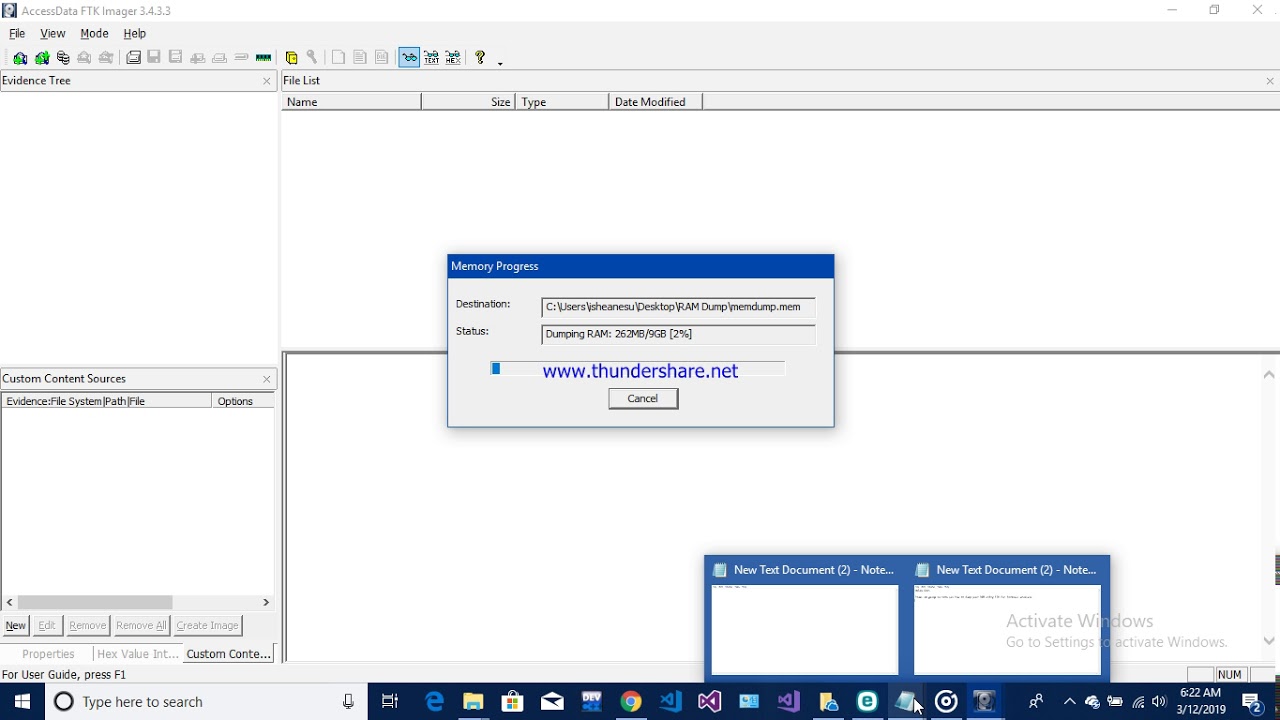
But I would like to go further and find the actual content of the windows. volatility does a great job at extracting useful information, including wire-view of the windows displayed at the time (using the command screenshot). Some classical security / hacking challenges include having to analyze the dump of the physical RAM of a system.


 0 kommentar(er)
0 kommentar(er)
